Algorithm/알고리즘 이론 | Algorithm

[알고리즘/Algorithm] 소수 판별 - 에라토스테네스의 체 / Sieve of Eratosthenes / BOJ 4948 베르트랑 공준 예제 풀이

Melody Blue 2025. 2. 20. 12:39
반응형

안녕하세요,

이번에는 소수 판별 알고리즘인 '에라토스테네스의 체'에 대해서 포스팅 해 보려고 합니다 !

에라토스테네스의 체 (Sieve of Eratosthenes)

에라토스테네스의 체는 여러 개의 수 중에서 소수를 빠르게 찾아내는 알고리즘입니다.

 

소수란?

1과 자기 자신만을 약수로 가지는 1보다 큰 자연수

입니다.

 

예를 들어, 2, 3, 5, 7, 11, 13, 17 등은 소수입니다.

 

◆ 기본 원리

 

1. 2부터 N까지의 모든 숫자를 소수라고 가정합니다.

2. 가장 작은 소수(2)부터 배수를 제거하여 소수가 아닌 숫자를 지웁니다.

3. 남아 있는 숫자들이 소수가 됩니다.

 

위와 같은 기본 원리를 바탕으로 소수 판별 알고리즘을 구현합니다.

 

예를 들어, N = 30까지의 소수를 찾는다고 하면, 아래와 같은 과정으로 소수를 구합니다.

// 1은 소수가 아니므로 제외
int[] arr = {2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20,
			21, 22, 23, 24, 25, 26, 27, 28, 29, 30};

// 2의 배수 제거 (2는 가장 작은 소수)
int[] arr = {2, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27, 29};

// 3의 배수 제거
int[] arr = {2, 3, 5, 7, 11, 13, 17, 19, 23, 25, 29};

// 5의 배수 제거
int[] arr = {2, 3, 5, 7, 11, 13, 17, 19, 23, 29};

더이상 남아있는 수의 배수가 없으므로 남아있는 숫자들은 모두 소수 입니다.

시간 복잡도 분석

그렇다면 시간복잡도는 어떻게 될까요?

 

◆ 단계별 분석

  1. 배열 초기화 → O(N)
  2. i를 돌며 배수를 제거 → 각 소수 p에 대해, N/p번 실행
    • 2의 배수 지우기: N/2번
    • 3의 배수 지우기: N/3번
    • 5의 배수 지우기: N/5번
    • …
    • 모든 과정 합산: N/2 + N/3 + N/5 + N/7 + ...
  3. 이 값은 O(N * log log N)으로 수렴

◆ 최종 복잡도

: O(N log log N) (거의 선형에 가까운 효율적인 알고리즘)

 

매번 모든 숫자마다 소인수분해 후 소수를 판별하는 건 시간이 오래걸리기 때문에,

가능할 경우는 이렇게 에라토스테네스의 체를 활용해서 소수를 판별해서 해결하고 있습니다.

에라토스테네스의 체 구현 및 증명

에라토스테네스의 체 알고리즘의 구현 과정은 아래와 같습니다.

  1. 배열을 만든다.
    • 0과 1은 소수가 아니므로 제외하고, 2부터 N까지 모든 수를 소수(true)로 가정.
  2. 2부터 시작하여 배수를 제거한다.
    • 2의 배수, 3의 배수, 5의 배수 등...
    • 자기 자신은 지우지 않되, 자신의 배수들은 소수가 아니므로 제거.
  3. N의 제곱근(√N)까지만 검사하면 된다.
    • 이유: 16 이하의 합성수(예: 15)는 작은 소수(3, 5)에서 이미 제거됨.
    • 즉, 최대 √N까지만 배수를 지우면 나머지는 자동으로 판별됨.

소스코드로 작성해보면 아래와 같습니다.

import java.util.Arrays;

public class SieveOfEratosthenes {
    public static void main(String[] args) {
        int N = 50; // 예제: 50까지의 소수 찾기
        boolean[] isPrime = new boolean[N + 1]; 
        
        Arrays.fill(isPrime, true); // 모든 수를 소수(true)로 초기화
        isPrime[0] = isPrime[1] = false; // 0과 1은 소수가 아님

        for (int i = 2; i * i <= N; i++) { // i가 √N 이하일 때까지 실행
            if (isPrime[i]) { // 소수인 경우
                for (int j = i * i; j <= N; j += i) { // i의 배수를 제거
                    isPrime[j] = false;
                }
            }
        }

        // 결과 출력
        System.out.println("소수 리스트:");
        for (int i = 2; i <= N; i++) {
            if (isPrime[i]) {
                System.out.print(i + " ");
            }
        }
    }
}

 

이해를 돕기 위해 주석을 기재하였습니다.

왜 √N까지만 검사하면 될까? (수학적 증명)

그렇다면 왜 √N까지만 검사하면 될까요?

 

합성수(소수가 아닌 수)는 항상 작은 소수의 배수로 먼저 지워집니다.

예를 들어, 15 = 3 × 5 인데,

  • 3에서 이미 15를 지웠음 → 5에서 또 지울 필요가 없습니다.
  • 그러므로 소수 p의 배수를 지울 때 p^2부터 지우면 충분합니다!

즉,

  • i * i ≤ N까지만 확인하면 됩니다.
  • i가 더 크면, 그 수의 배수는 이미 이전에 처리되었기 때문입니다.

예제 문제 풀이: BOJ 4948 베르트랑 공준

에라토스테네스의 체에 관한 가장 기본적인 예제는 BOJ 2960: 인데요,

한 번 풀어보시는 것을 추천드립니다! :)

BOJ 2960 에라토스테네스의 체

https://www.acmicpc.net/problem/2960

 

여기서는 한 단계 더 나아가서 에라토스테네스의 체 + 탐색이 들어간 문제를 예제로 풀어보겠습니다.

 

예제: BOJ 4948 베르트랑 공준

https://www.acmicpc.net/problem/4948

 

문제에서 구해야 할 것은 결국

'자연수 n이 주어졌을 때, n보다 크고(초과) 2n보다 작거나 같은(이하) 소수의 개수 구하기' 입니다.

이 때, 문제의 조건이자 '베르트랑 공준'명제는 아래와 같습니다.

임의의 자연수 n에 대하여, n보다 크고, 2n보다 작거나 같은 소수는 적어도 하나 존재한다.

 

즉, 우리가 구해야하는 결과 값은 항상 1 이상이라는 것을 알 수 있습니다.

그럼 다음과 같이 구현해야할 내용을 설계해볼 수 있습니다.

 

◆ 구현 설계

1. 입력 받기

   - 입력이 테스트 케이스들로 이루어져있고, 0이 입력해야 입력이 종료됨

   - 따라서 0이 입력되기 전 까지 계속 입력을 받아야 함

   - 시간복잡도를 고려한 설계 필요

2. 소수 구하기

   - 에라토스테네스의 체로 미리 모든 범위의 소수를 구해놓기 (반복해서 소수를 판별하지 않아도 됨)

   - 배열에 저장해두고 매 테스트 케이스마다 탐색 하도록 할 수 있음

3. 소수 갯수 확인

   - 케이스마다 n + 1 부터 2*n 까지 소수판별이 된 배열을 탐색하면서 갯수 확인

 

이제 소스와 함께 구현방식을 살펴보겠습니다.

 

* 에라토스테네스의 체 구현

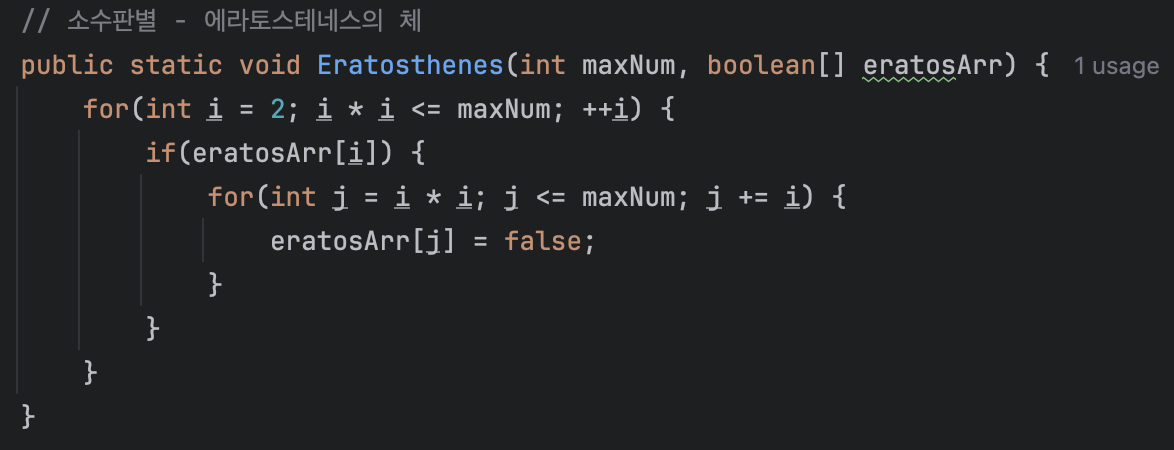
// 소수판별 - 에라토스테네스의 체
    public static void Eratosthenes(int maxNum, boolean[] eratosArr) {
        for(int i = 2; i * i <= maxNum; ++i) {
            if(eratosArr[i]) {
                for(int j = i * i; j <= maxNum; j += i) {
                    eratosArr[j] = false;
                }
            }
        }
    }

첫 번째 반복문에서 i의 범위가 2에서 시작하여 i*i가 maxNum까지일 때 입니다.

이는 위에서 증명한 대로 √n 까지 탐색하기 위함입니다.

 

그렇다면 왜 두 번째 반복문에서는 j = i*i 로 시작했을까요?

 

  • i가 소수라면, i의 배수를 제거해야 합니다.
  • 하지만 i보다 작은 수의 배수는 이미 앞 단계에서 제거되었습니다.
    → 굳이 j = i + i (i의 두 배)부터 시작할 필요가 없습니다.

만약 j = i + i 부터 시작할 경우 불필요한 연산이 발생합니다.

예를 들면, i = 3일 때 j = 6부터 시작하면, 6은 이미 i = 2일 때 2의 배수로 처리되었습니다.
   → 불필요한 반복 연산이 발생!

 

즉, j = i * i로 시작하면 중복 제거 연산을 하지 않아도 됩니다.

 

소스 캡쳐본도 첨부하였습니다. :)

에라토스테네스의 체 소스

 

* 테스트케이스 별 탐색 구현

// 테스트케이스 별 탐색
            for(String now : queries) { // 테스트케이스는 queries에 저장해둠
                int count = 0;
                int start = Integer.parseInt(now);
                for(int i = start + 1; i <= start * 2; ++i) { // 탐색 범위 확인!
                    if(eratosArr[i]) { // 소수일 경우 count 증가
                        count++;
                    }
                }
                System.out.println(count);
            }

테스트케이스 별 탐색은 탐색 범위만 잘 확인해주면 어렵지 않습니다.

모든 테스트케이스에 대하여 말 그대로 소수를 세어주면 됩니다.

이미 에라토스테네스의 체 알고리즘을 소수를 판별해 둔 배열이 있기 때문에(eratosArr) 테스트케이스 당 O(n)으로 탐색하여 확인할 수 있습니다.

이렇게 소수판별 알고리즘인 '에라토스테네스의 체'에 대해서 정리해보았습니다.

'소수 판별' 을 말로만 들을 땐 간단해 보였지만,

막상 구현하려니 시간복잡도가 높아져서 고민이었는데 에라토스테네스의 체를 활용하니 훨씬 시간복잡도를 줄여서 구현할 수 있었습니다.

제가 궁금한 것들까지 정리해보았는데요,

저와 같이 공부하고 계신 분들께도 도움이 될 수 있길 바랍니다!

 

다들 알고리즘 공부 화이팅입니다~!

반응형