[알고리즘/Algorithm] 이분 탐색(이진 탐색) / Binary Search Algorithm 이론 정리 및 예제 풀이

알고리즘 문제풀이를 공부하면서, 역시나 정리가 필수라는 생각이 계속 들었습니다!

차근차근 정리해보겠습니다 :)

이번에는 이분 탐색(이진 탐색) 인 Binary Search에 대해 정리해보겠습니다.

이분 탐색(이진 탐색) / 바이너리 서치(Binary Search) 알고리즘이란?

이분 탐색은 '두 영역으로 나눠서 탐색'하는 탐색 방법 입니다.

정렬된 데이터에서 원하는 값을 빠르게 찾는 알고리즘인데요,

데이터를 반 씩 나눠서 탐색하기 때문에 검색 속도가 매우 빠르며 대규모 데이터 처리에 적합합니다.

배열에서 특정 원소를 찾아야 할 때, 배열의 길이가 너무 길 경우 (원소 개수가 너무 많을 경우)에는

배열의 모든 원소를 확인하는 작업이 굉장히 오래걸릴 수 있습니다.

그럴 때, 두 영역을 비교해서 타겟 원소의 '영역'을 찾아가며 범위를 줄여가는 방법인 이분탐색을 사용할 수 있습니다.

이분 탐색은 대소비교 등을 통해 해당 원소가 포함된 영역을 찾아나가는 작업이므로,

아래와 같은 전제조건이 있습니다.

전제조건

1. 배열이 오름차순(조건에 따라 내림차순)으로 정렬되어있어야 함

2. Random Access가 가능해야 함: 배열에서 처럼, 인덱스 등으로 빠르게 데이터에 접근할 수 있어야 함

(랜덤 액세스란 데이터를 저장하거나 읽는 과정에서 특정 위치에 직접 접근할 수 있는 능력을 말합니다.)

따라서 저는 구현시 아래와 같은 순서로 설계합니다.

개발 설계

1. 배열 정렬

2. 이분탐색 범위 결정

3. 탐색 조건 확인

이 순서로 아래 예시에서 설계해보겠습니다.

이분탐색은 왜 사용하는 걸까요? 다음과 같은 이유로 이분 탐색을 사용합니다.

이분 탐색을 사용하는 이유

데이터가 정렬되어 있는 경우 탐색 속도가 O(n)인 선형 탐색에 비해 훨씬 빠름.
배열이나 리스트뿐만 아니라, 문제의 값이 단조증가/단조감소 형태로 추측 가능할 때도 사용 가능 (예: 최소값, 최대값, 특정 조건 만족 여부 탐색 등).

범위를 반으로 나눠서, 목표 값에 도달/포함 여부에 따라서 범위를 찾아가므로 속도가 훨씬 빠릅니다.

(ex. 그래서 예전에 술게임 중에 소주뚜껑 숫자 맞추는 것도 이분탐색 하는 친구가 있었죠,,)

참고로, 여러 조건 및 특성상의 한계도 존재합니다.

이분탐색의 한계

데이터가 정렬되지 않은 경우 사용할 수 없음.
정렬을 유지하는 비용이 탐색 속도를 상쇄할 수 있음 (데이터 추가, 삭제가 빈번한 경우).
데이터가 연결 리스트와 같이 순차 접근만 가능한 자료구조에 저장된 경우 비효율적.
다차원 데이터(예: 2D 행렬)의 경우 사용하려면 특정 변형이 필요함.

그럼 다음으로는 작동 원리에 대한 내용을 정리해보겠습니다.

이분탐색 작동 원리

이분탐색의 작동 원리는 다음과 같습니다.

여기서는 찾아야하는 수를 target, target을 찾아야할 수 배열을 arr[]라고 하겠습니다.

1. 탐색 범위의 최소값(left)과 최대값(right)을 설정합니다. - 여기서는 인덱스로 사용됩니다.

int left = 0; // 탐색 시작범위 (최소값)
int right = 100000; // 탐색 끝 범위 (최대값)

2. 중간값(mid)을 구합니다. - mid도 left, right과 마찬가지로 중간 인덱스로 사용됩니다.

int mid = (left + right) / 2;

3. 조건을 확인합니다.

arr[mid] == target: 값을 찾았으므로 중간값 반환.
arr[mid] < target: 탐색 범위를 오른쪽으로 이동. low = mid + 1
arr[mid] > target: 탐색 범위를 왼쪽으로 이동. high = mid - 1

if(arr[mid] == target) {
	// 확인 조건
    answer = mid;
} else if(arr[mid] < target) {
	left = mid + 1;
} else {
	right = mid - 1;
}

예를 들어,

target = 32, arr[] = {2, 4, 8, 16, 32, 64, 128, 256}; 라고 하면, 아래 표와 같은 순서로 탐색하게 됩니다.

탐색 횟수	1번 째	2번 째	3번 째
left	0	4	4
right	7	7	4
mid	3	5	4
arr[mid]	16	64	32

이렇게 총 3번 탐색 이후에 32를 찾게 됩니다.

선형 탐색의 경우에는 5번 탐색이 필요하니, 탐색 횟수에서도 차이가 나는 것을 볼 수 있습니다.

4. 종료 조건

탐색 범위가 low≤high 를 만족하지 않으면 종료합니다.

while(left <= right) {
	// 이분탐색 조건 확인 및 범위 이동 부분
}

이분탐색 시간복잡도

그렇다면 시간복잡도는 어떻게 될까요?

시간복잡도

1. 최선의 경우 (Best Case): O(1) (찾으려는 값이 중앙값인 경우)

2. 평균 및 최악의 경우 (Average & Worst Case): O(log⁡n)

데이터의 크기가 절반씩 줄어들기 때문에, 시간 복잡도는 로그 형태입니다.
n개의 데이터가 있을 때 최대 비교 횟수는 log⁡(2)n

1. 최선의 경우에는 찾으려는 값이 바로 arr[mid]로 인덱스로 바로 접근이 가능하기 때문에 O(1)입니다.

2. 평균적으로 n개의 데이터 중 2개의 영역으로 나눠서, 즉 탐색 범위를 반으로 줄여서! 찾아나가므로 로그_2의 N이 되게 됩니다.

배열 크기가 일 때, 탐색 첫 단계에서 배열은 n/2로 줄어듭니다.
두 번째 단계에서는 n/4, 세 번째 단계에서는 n/8...
k번째 단계에서 배열 크기가 n/2^k가 됩니다.

탐색이 끝나는 조건은 배열 크기가 1이 되는 순간: n/2^k=1

양변에 2^k를 곱하면: n = 2^k

양변에 log_2를 취하면: log_2(n) = k

따라서, 탐색 단계 수 k는 log_2(n)에 비례합니다.

탐색 단계 수 k가 입력 크기 n의 로그에 비례하므로:

이분 탐색 예시 코드 - Java

nums라는 숫자 배열에서 target을 찾는 이분 탐색 소스입니다.

아래 코드 예시는 nums가 오름차순 정렬임을 가정하고 작성하였습니다.

public static int binarySearch(int[] nums, int target) {
        int answer = 0;
        int left = 0;
        int right = nums.length - 1;

        while(left <= right) {
            int mid = (left + right) / 2; // mid 구하기
            if(nums[mid] == target) { // 조건 만족
                answer = 1;
                break;
            }
            if(nums[mid] > target) { // 범위 줄여가기
                right = mid - 1;
            } else {
                left = mid + 1;
            }
        }

        return answer;
    }

이분 탐색 소스 개선 - 오버플로우 방지

한 가지 주의할 점은, 중간값인 mid를 계산할 때 오버플로우가 발생할 수 있다는 점 입니다.

따라서 중간값 계산을 아래와 같이 바꿀 수 있습니다.

// method 1
int mid1 = (left + right) / 2;
// method 2
int mid = left + (right-left)/2;

이는 중간값 계산을 보다 정확하게 수행하기 위함입니다.

기존 방식인 method 1은 정수 오버플로우의 가능성이 있습니다.

low + high에서 두 값의 합이 정수의 범위를 넘어가는 경우 문제가 발생합니다.
예를 들어, Java에서 정수의 최대값 2^{31} - 1 = 2,147,483,647을 초과하면 오버플로우가 발생하여 잘못된 값이 나옵니다.

method 2의 경우

는 항상 low와 high의 차이값이므로 high + low보다 작아 오버플로우를 방지할 수 있습니다.
결과는 동일한 중간값을 계산합니다.

수학적 증명

method 2가 정말 중간값이 되는 지 확인하기 위한 수학적 증명입니다.

mid = left + (right-left)/2

= left + right/2 - left/2

= (2left + right - left)/2

= (left + right)/2

결국 mid = (left + right)/2와 동일하다는 것을 알 수 있습니다.

따라서 mid 를 수정하면 코드는 아래와 같이 바뀝니다.

public static int binarySearch(int[] nums, int target) {
        int answer = 0;
        int left = 0;
        int right = nums.length - 1;

        while(left <= right) {
            int mid = left + (right - left) / 2; // 중간값 계산 시 오버플로우 방지
            if(nums[mid] == target) {
                answer = 1;
                break;
            }
            if(nums[mid] > target) {
                right = mid - 1;
            } else {
                left = mid + 1;
            }
        }

        return answer;
    }

예제 문제 풀이 : BOJ 1920 수 찾기

예제:

https://www.acmicpc.net/problem/1920

위 문제는 가장 기본적인 이분탐색 문제입니다.

즉, 주어진 N개의 수가 들어있는 배열 A에서, M개의 숫자가 A에 존재하는지 찾는 문제입니다.

'존재하는지' 여부만 판단하면 되므로

1. 배열을 정렬해도 되고

2. 인덱스로 랜덤엑세스가 가능합니다.

따라서 이분탐색으로 풀 수 있습니다.

아래에는 코드를 첨부하였습니다.

public static void main(String[] args) {
        Scanner input = new Scanner(System.in);
        // 입력 부분
        int n = input.nextInt();
        int[] arrA = new int[n];
        for(int i=0; i<n; i++) {
            arrA[i] = input.nextInt();
        }
        int m = input.nextInt();
        int[] arrM = new int[m];
        for(int i=0; i<m; i++) {
            arrM[i] = input.nextInt();
        }

        Arrays.sort(arrA); // 오름차순 정렬

        for(int i = 0; i < m; ++i) {
            System.out.println(binarySearch(arrA, arrM[i]));
        }
    }

    public static int binarySearch(int[] arr, int target) {
        int answer = 0;
        int left = 0, right = arr.length - 1;

        while(left <= right) { // 탐색 범위
            int mid = left + (right - left) / 2;
            if(arr[mid] == target) { // 찾은 경우
                answer = 1;
                break;	// 탐색 중지 (완료)
            }
            if(arr[mid] < target) {
                left = mid + 1;
            } else{
                right = mid - 1;
            }
        }

        return answer;
    }

아래는 코드 구현 캡쳐본입니다.

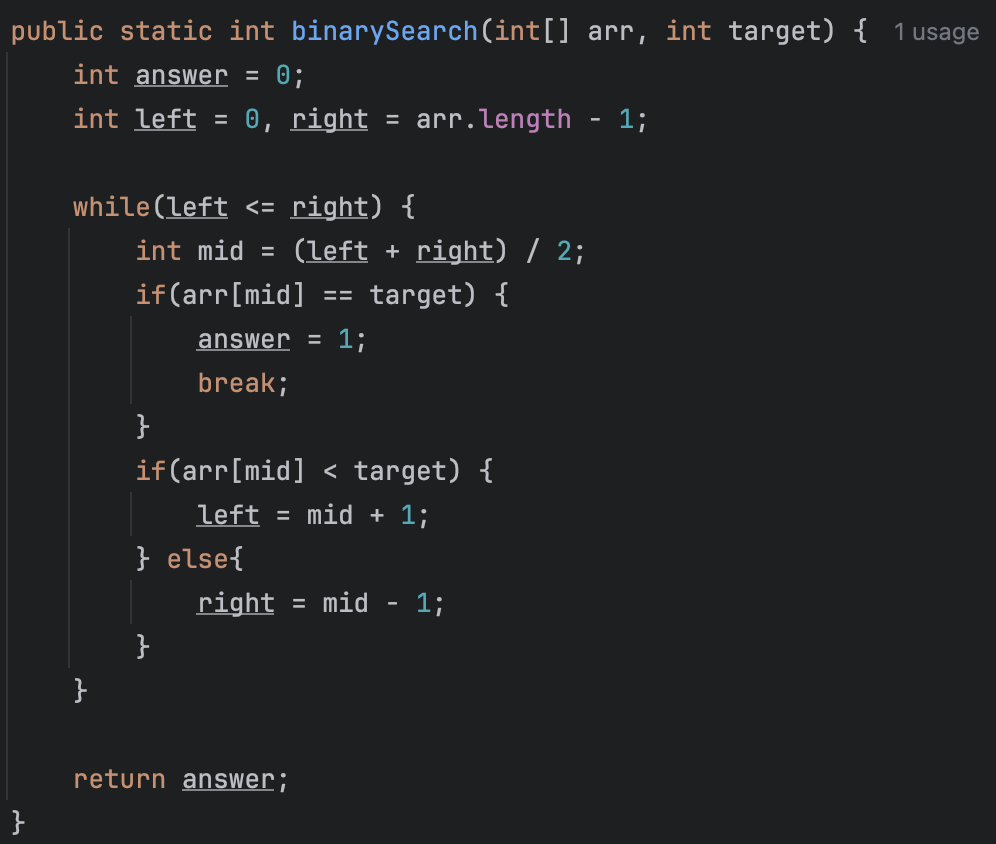
아래 조건은 탐색 조건인데요,

찾으려는 사항을 조건문으로 확인해줍니다.

if(arr[mid] == target) { // 찾은 경우
    answer = 1;
    break;	// 탐색 중지
}

문제에서 '해당 숫자의 존재 여부'만 확인하면 되기 때문에,

숫자가 존재한다면 더 탐색할 필요가 없어 break문을 넣어주었습니다.

이렇게 알고리즘 문제풀이 방식 중 하나인 '이분탐색(Binary Search)'에 대해서 정리해보았습니다.

예전에 알고리즘 공부할 때 완전탐색 공부 이후로 이어서 공부했던 알고리즘이었는데요,

최근 다시 정리해보려고 하니 많이 까먹었더라고요ㅎㅎ

그래서 이번 기회에 궁금했던 사항을 포함해서 작성해보았습니다.

나중에 다시 기초 사항을 공부할 때도 도움이 되길 바라며 작성했는데요,

저와 같이 알고리즘 이론을 찾아보시는 분들께도 도움이 되셨길 바랍니다!

'Algorithm > 알고리즘 이론 | Algorithm' 카테고리의 다른 글

[알고리즘/Algorithm] 동적계획법 Dynamic Programming / BOJ 9095 1, 2, 3 더하기 & BOJ 2839 설탕 배달 (2)	2025.03.26
[알고리즘/Algorithm] 소수 판별 - 에라토스테네스의 체 / Sieve of Eratosthenes / BOJ 4948 베르트랑 공준 예제 풀이 (1)	2025.02.20
[알고리즘/Algorithm] 완전탐색 / Brute-Force Algorithm 이론 정리 및 예제 풀이 (4)	2024.11.20

MelodyBlue

[알고리즘/Algorithm] 이분 탐색(이진 탐색) / Binary Search Algorithm 이론 정리 및 예제 풀이

이분 탐색(이진 탐색) / 바이너리 서치(Binary Search) 알고리즘이란?

이분탐색 작동 원리

이분탐색 시간복잡도

이분 탐색 예시 코드 - Java

이분 탐색 소스 개선 - 오버플로우 방지

예제 문제 풀이 : BOJ 1920 수 찾기

'Algorithm > 알고리즘 이론 | Algorithm' 카테고리의 다른 글

티스토리툴바

[알고리즘/Algorithm] 이분 탐색(이진 탐색) / Binary Search Algorithm 이론 정리 및 예제 풀이

이분 탐색(이진 탐색) / 바이너리 서치(Binary Search) 알고리즘이란?

이분탐색 작동 원리

이분탐색 시간복잡도

이분 탐색 예시 코드 - Java

이분 탐색 소스 개선 - 오버플로우 방지

예제 문제 풀이 : BOJ 1920 수 찾기

'Algorithm > 알고리즘 이론 | Algorithm' 카테고리의 다른 글

관련글

티스토리툴바