안녕하세요!
이번에는 바로! 알고리즘 문제풀이(Algorithm Problem Solving)의 꽃이라고 불리는 동적 계획법에 대해서 정리해보려고 합니다 :0

분할정복이나 수학 관련 알고리즘을 먼저 공부할까 했는데, 문제를 풀어나가다 보니 DP에 대해서 먼저 정리하고 싶어졌습니다 ㅎㅎ
난이도가 있는 문제가 꽤 많이 나와서, 이 김에 정리해두려고 합니다!ㅎㅎ
동적계획법(Dynamic Programming) 이란?
먼저 동적계획법(Dynamic Programming; 다이나믹 프로그래밍)이 무엇일까요?
동적계획법은 복잡한 문제를 작은 부분으로 나누고, 이를 저장하여 중복 계산을 줄이는 기법입니다.
즉, 분할정복과 비슷하지만 중복되는 부분의 결과값을 저장하고 재사용하는 과정이 추가된 것입니다.
■ DP를 사용하는 경우
- 중복되는 부분 문제(Overlapping Subproblems)
- 동일한 작은 문제(부분 문제)가 여러 번 반복해서 등장하는 경우
- 최적 부분 구조(Optimal Substructure)
- 부분 문제의 최적해를 이용해 전체 문제의 최적해를 구할 수 있는 경우
예시: 피보나치 수열
...
F(6) = F(5) + F(4)
F(5) = F(4) + F(3)
F(4) = F(3) + F(2)
F(3) = F(2) + F(1)이처럼 F(4), F(3) 등의 같은 계산이 중복되어 사용되므로 DP를 사용할 수 있습니다.
동적계획법(DP; Dynamic Programming) 접근법
DP는 Top-Down 방식, Bottom-Up 방식의 두 가지로 나뉩니다.
(1) Top-Down 방식 (메모이제이션)
- 재귀 + 캐싱을 사용하여 해결하는 방법
- 한 번 계산한 값을 저장해놓고 재사용 -> 중복 연산 방지
- 함수 호출 시마다 필요한 부분만 계산 -> 불필요한 계산을 줄일 수 있음
- 예시: 피보나치 수열 - Top Down 방식 구현
- memo.put(n, result);를 통해 중복된 계산을 저장하여 시간을 절약
import java.util.HashMap;
public class Fibonacci {
static HashMap<Integer, Long> memo = new HashMap<>();
static long fib(int n) {
if (n <= 1) return n;
if (memo.containsKey(n)) return memo.get(n); // 결과값이 이미 있을 경우
long result = fib(n - 1) + fib(n - 2);
memo.put(n, result); // 결과값 저장
return result;
}
public static void main(String[] args) {
System.out.println(fib(50)); // 12586269025
}
}
(2) Bottom-Up 방식 (Tabulation)
- 반복문을 사용해 작은 문제부터 차근차근 해결하는 방식
- 배열에 값을 저장하며 문제를 해결 (메모이제이션 없이 해결)
- 시간과 공간 효율성이 더 좋음 (재귀 호출 없이 진행)
- 예시: 피보나치 수열 - Bottom Up 방식 구현
- dp[i]에 값을 저장하면서 반복문으로 값을 채워나가는 방식
public class FibonacciBottomUp {
public static void main(String[] args) {
int n = 50;
long[] dp = new long[n + 1];
dp[0] = 0;
dp[1] = 1;
for (int i = 2; i <= n; i++) {
dp[i] = dp[i - 1] + dp[i - 2];
}
System.out.println(dp[n]); // 12586269025
}
}
DP는 다양한 알고리즘에 활용이 가능한, 중요한 개념이므로 잘 공부해둬야겠어요 !

동적 계획법(DP; Dynamic Programming) 시간복잡도
■ 피보나치 수열 문제의 경우
* 단순 재귀 (O(n^2)) -> 비효율적
: 재귀적으로 구현을 한다면 중복계산이 많아 O(n*2)가 됩니다.
* DP(Top-down, Bottom-up) -> O(n)
: fibonacci(n) 을 한 번 씩만 계산 & 저장 -> O(n)이 됨!
-> 즉, 중복 계산을 피하면서 성능향상이 가능합니다.
■ 일반적인 DP의 시간복잡도 분석
: DP를 활용하는 알고리즘은 여러가지가 있습니다.
간단히 시간복잡도를 정리해보자면 아래와 같습니다.
| 알고리즘 | 일반적인 시간복잡도 |
| (대조군) 피보나치 (재귀) | O(n^2) |
| 피보나치 (DP) | O(n) |
| 0/1 Knapsack (배낭문제) | O(nm) (n: 아이템 개수, m: 배낭 용량) |
| 최장 공통 부분 수열 (LCS) | O(nm) (n, m: 문자열 길이) |
| 동전 거스름돈 문제 | O(nm) (n: 동전 개수, m: 목표 금액) |
★ DP는 보통 O(N) ~ O(N²) 수준으로 효율적입니다!
Tabulation vs Memoization
공부하다보니 저도 궁금해졌습니다.
" Tabulation 과 Memoization 은 다른 것인가? "
둘 모두 DP 에서 중복 연산을 줄이기 위해 값을 저장하는 기법이지만 접근 방식이 다릅니다.
■ Memoization vs. Tabulation 비교 정리
두 가지 기법을 표로 비교해보자면 아래와 같습니다.
| 개념 | Memoization(메모이제이션) | Tabulation(타뷸레이션) |
| 접근 방식 | Top-Down (재귀) | Bottom-Up (반복) |
| 값 저장 방식 | 필요할 때만 계산 후 저장 | 처음부터 배열을 채우며 저장 |
| 코딩 스타일 | 재귀 + 저장 | 반복문 + 저장 |
| 메모리 사용량 | 재귀 호출 스택을 사용 (Stack Overflow 가능) | 배열에 값을 채우며 진행 (메모리 예측 가능) |
| 사용 시점 | 큰 문제를 먼저 풀고, 작은 문제를 저장 | 작은 문제부터 차례로 해결하며 저장 |
| 성능 | 재귀 호출로 인해 오버헤드 발생 가능 | 반복문을 사용하여 성능 최적화 가능 |
✔ 즉, 타뷸레이션은 메모이제이션과 같은 저장 개념을 사용하지만, 저장 방식이 다르기 때문에 별도의 기법으로 구분됩니다.
■ 예제 코드 비교
1) 메모이제이션 (Memoization) - Top-Down (재귀)
: 필요할 때마다 값을 저장하며 계산 (Lazy Evaluation)
* 예제 코드는 피보나치 수열을 구하는 로직입니다.
import java.util.Arrays;
public class FibonacciMemoization {
static int[] dp = new int[100]; // 저장 배열
public static int fibonacci(int n) {
if (n <= 1) return n;
if (dp[n] != -1) return dp[n]; // 저장된 값이 있으면 반환
return dp[n] = fibonacci(n - 1) + fibonacci(n - 2); // 저장 후 반환
}
public static void main(String[] args) {
Arrays.fill(dp, -1); // 초기화
System.out.println(fibonacci(10)); // 55
}
}위 소스는 fibonacci(n)이 필요할 때만 계산하며, dp[n]에 계산된 값을 저장합니다.
단, 재귀 호출이 많아지면 스택 오버플로우 위험 존재합니다.
2) 타뷸레이션 (Tabulation) - Bottom-Up (반복문)
: 작은 문제부터 차근차근 계산하여 저장
public class FibonacciTabulation {
public static int fibonacci(int n) {
if (n <= 1) return n;
int[] dp = new int[n + 1]; // 저장 배열
dp[0] = 0;
dp[1] = 1;
for (int i = 2; i <= n; i++) {
dp[i] = dp[i - 1] + dp[i - 2]; // 작은 문제부터 차례로 계산
}
return dp[n];
}
public static void main(String[] args) {
System.out.println(fibonacci(10)); // 55
}
}이 로직으로는 반복문을 사용하여 작은 문제부터 해결합니다.
반복문을 통한 호출로, 재귀 호출이 없어 스택 오버플로우 위험이 없습니다.
추가로, 메모리 사용량을 더 효율적으로 조절 가능합니다.
■ 시간복잡도 비교
| 방법 | 최악의 시간복잡도 | 특징 |
| 일반 재귀 (Memoization X) | O(2ⁿ) | 중복 연산 많음 |
| 메모이제이션 (Top-Down) | O(N) | 필요할 때만 저장 (Lazy Evaluation) |
| 타뷸레이션 (Bottom-Up) | O(N) | 처음부터 모든 값을 저장 |
💡 타뷸레이션과 메모이제이션 모두 O(N)이지만, 타뷸레이션이 호출 오버헤드가 없어 더 빠릅니다!
◆ 정리: "타뷸레이션도 결국 메모이제이션인가?"
✔ 둘 다 "이전에 계산한 값을 저장하는 개념"을 사용하므로 비슷합니다.
하지만, 메모이제이션은 "필요할 때 저장" (Top-Down), 타뷸레이션은 "처음부터 저장" (Bottom-Up)
✔ 둘 다 시간복잡도는 O(N)이지만, 타뷸레이션이 호출 오버헤드가 없어 더 빠릅니다.
✔ 메모이제이션은 재귀 기반이라 스택 오버플로우 가능성 존재, 타뷸레이션은 반복문이라 안정적입니다.
즉, "타뷸레이션도 저장을 하지만, 구현 방식과 접근 방식이 다르기 때문에 메모이제이션과 별개의 개념으로 본다!" 라고 정리할 수 있습니다.
예제 문제 풀이: BOJ 9095 1, 2, 3 더하기 / BOJ 2839 설탕 배달
이번엔 두 가지 문제를 예제로 풀어보았습니다.
난이도가 있는 만큼 여러가지 문제를 풀어보면 좋을 듯 합니다.

* 예제 문제: BOJ 9095 1, 2, 3 더하기
링크: https://www.acmicpc.net/problem/9095
문제:
정수 n을 1, 2, 3의 합으로 나타낼 수 있는 방법의 수 구하기 입니다.
문제에서는 1, 2, 3을 더하는 순서도 개별 방법의 수로 취급합니다.
(1 + 2와 2 + 1은 모두 결과가 3이지만 다른 방법의 수로 여깁니다.)
example:
n = 4 일 때, 아래와 같이 작성해볼 수 있습니다.
| n | n = 1 | n = 2 | n = 3 | n = 4 |
| n을 만드는 경우 | 1 | 1 + 1 | 1 + 1 + 1 | 1 + 1 + 1 + 1 |
| 2 | 1 + 2 | 1 + 1 + 2 | ||
| 3 | 1 + 2 + 1 | |||
| 2 + 1 + 1 | ||||
| 2 + 2 | ||||
| 1 + 3 | ||||
| 3 + 1 | ||||
| 방법의 수 | 1 | 2 | 3 | 7 |
결과는 7인데요, 규칙을 파악하기 위해 좀 더 작성해보겠습니다.

5를 만드는 경우의 수는
4를 만드는 경우들에 + 1을 해주거나
3을 만드는 경우들에 + 2를 해주거나
2를 만드는 경우들이 + 3을 해주는 경우들로 구성되어있는 것을 확인할 수 있습니다.
각각 구분하기 쉽게 색으로 표시해보았습니다!

| n | n = 1 | n = 2 | n = 3 | n = 4 | n = 5 |
| n을 만드는 경우 | 1 | 1 + 1 | 1 + 1 + 1 | 1 + 1 + 1 + 1 | 1 + 1 + 1 + 1 + 1 |
| 2 | 1 + 2 | 1 + 1 + 2 | 1 + 1 + 1 + 2 | ||
| 2 + 1 | 1 + 2 + 1 | 1 + 1 + 2 + 1 | |||
| 3 | 2 + 1 + 1 | 1 + 2 + 1 + 1 | |||
| 2 + 2 | 2 + 1 + 1 + 1 | ||||
| 1 + 3 | 1 + 2 + 2 | ||||
| 3 + 1 | 2 + 1 + 2 | ||||
| 2 + 2 + 1 | |||||
| 1 + 1 + 3 | |||||
| 1 + 3 + 1 | |||||
| 3 + 1 + 1 | |||||
| 2 + 3 | |||||
| 3 + 2 | |||||
| 방법의 수 | 1 | 2 | 4 | 7 | 13 |
따라서 n = 5를 1, 2, 3 더하기로 나타낼 수 있는 방법의 수는 13개 입니다.
한 번 더 해볼까요?
6을 만드는 경우의 수는
5를 만드는 경우들에 + 1을 해주거나
4를 만드는 경우들에 + 2를 해주거나
3을 만드는 경우들이 + 3을 해주는 경우들로 구성되어있는 것을 확인할 수 있습니다.
| n | n = 1 | n = 2 | n = 3 | n = 4 | n = 5 | n = 6 |
| n을 만드는 경우 | 1 | 1 + 1 | 1 + 1 + 1 | 1 + 1 + 1 + 1 | 1 + 1 + 1 + 1 + 1 | 1 + 1 + 1 + 1 + 1 + 1 |
| 2 | 1 + 2 | 1 + 1 + 2 | 1 + 1 + 1 + 2 | 1 + 1 + 1 + 1 + 2 | ||
| 2 + 1 | 1 + 2 + 1 | 1 + 1 + 2 + 1 | 1 + 1 + 1 + 2 + 1 | |||
| 3 | 2 + 1 + 1 | 1 + 2 + 1 + 1 | 1 + 1 + 2 + 1 + 1 | |||
| 2 + 2 | 2 + 1 + 1 + 1 | 1 + 2 + 1 + 1 + 1 | ||||
| 1 + 3 | 1 + 2 + 2 | 2 + 1 + 1 + 1 + 1 | ||||
| 3 + 1 | 2 + 1 + 2 | 1 + 1 + 2 + 2 | ||||
| 2 + 2 + 1 | 1 + 2 + 1 + 2 | |||||
| 1 + 1 + 3 | 1 + 2 + 2 + 1 | |||||
| 1 + 3 + 1 | 2 + 1 + 1 + 2 | |||||
| 3 + 1 + 1 | 2 + 1 + 2 + 1 | |||||
| 2 + 3 | 2 + 2 + 1 + 1 | |||||
| 3 + 2 | 1 + 1 + 1 + 3 | |||||
| 1 + 1 + 3 + 1 | ||||||
| 1 + 3 + 1 + 1 | ||||||
| 3 + 1 + 1 + 1 | ||||||
| 1 + 2 + 3 | ||||||
| 1 + 2 + 3 | ||||||
| 2 + 1 + 3 | ||||||
| 2 + 3 + 1 | ||||||
| 3 + 1 + 2 | ||||||
| 3 + 2 + 1 | ||||||
| 2 + 2 + 2 | ||||||
| 3 + 3 | ||||||
| 방법의 수 | 1 | 2 | 4 | 7 | 13 | 24 |
따라서 n = 6를 1, 2, 3 더하기로 나타낼 수 있는 방법의 수는 24개 입니다.
규칙을 보면서 이전에 구한 결과를 저장해두고 활용함을 알 수 있습니다.
이를 바탕으로 만든 점화식은 아래와 같습니다.
dp[i] = dp[i-1] + dp[i-2] + dp[i-3];점화식을 찾은 이후에는
1. 입력
2. 점화식으로 값 구하기
3. 원하는 최종 값 출력
단계로 구현을 완료하였습니다.
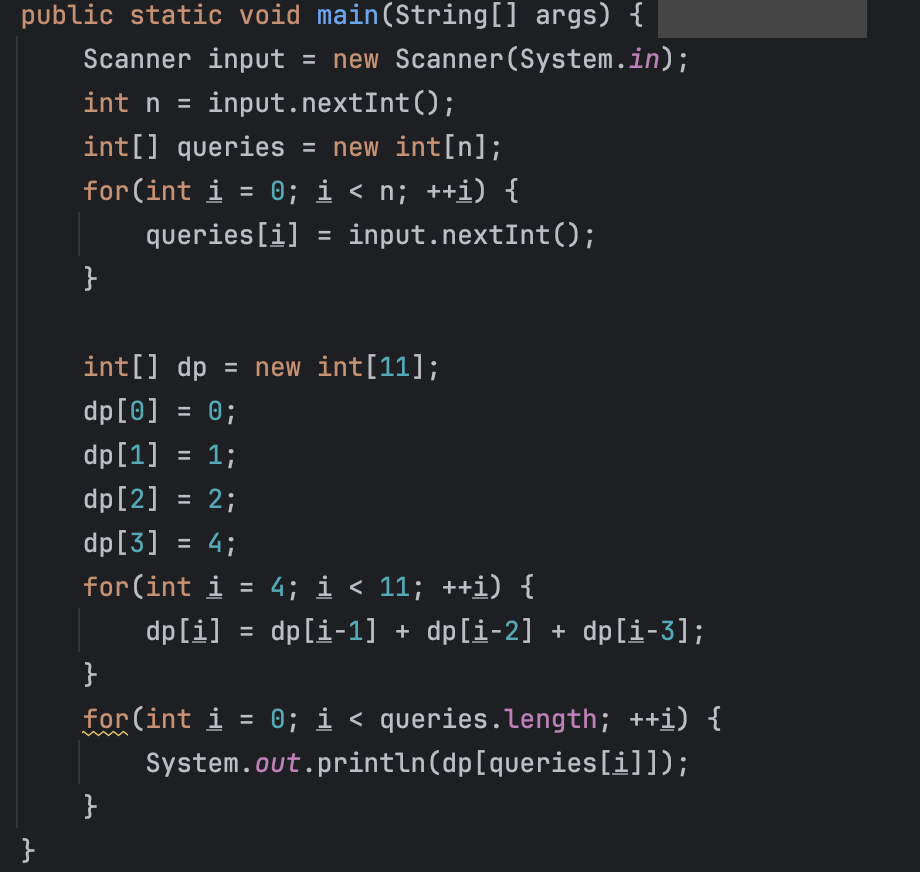
동적계획법 구현 / 전체 소스 코드
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner input = new Scanner(System.in);
int n = input.nextInt();
int[] queries = new int[n];
for(int i = 0; i < n; ++i) {
queries[i] = input.nextInt();
}
int[] dp = new int[11];
dp[0] = 0;
dp[1] = 1;
dp[2] = 2;
dp[3] = 4;
for(int i = 4; i < 11; ++i) {
dp[i] = dp[i-1] + dp[i-2] + dp[i-3];
}
for(int i = 0; i < queries.length; ++i) {
System.out.println(dp[queries[i]]);
}
}
}생각보다 코드가 간결하게 완성하였습니다.

* 예제 문제: BOJ 2839 설탕 배달
링크: https://www.acmicpc.net/problem/2839
문제:
3kg, 5kg 설탕 봉지가 있습니다.
입력된 nkg의 설탕을 정확히 배달해야 할 때,
배달할 설탕 봉지의 최소 수를 구하는 문제입니다.
index를 설탕 kg수라고 정의하고 가능한 경우의 수를 작성해보면 아래와 같이 작성해볼 수 있습니다.
| index | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| dp[index] | -1 | -1 | 1 | -1 | 1 | 2 | -1 | 2 | 3 | 2 |
| kg 구성 | - | - | 3kg | - | 5kg | 3kg + 3kg | - | 3kg + 5kg | 3kg + 3kg + 3kg | 5kg + 5kg |
| 11 | 12 | 13 | 14 | 15 | 16 |
| 3 | 4 | 3 | 4 | 3 | 4 |
| 3kg + 3kg + 5kg | 3kg + 3kg + 3kg + 3kg | 3kg + 5kg + 5kg | 3kg + 3kg + 5kg + 3kg | 5kg + 5kg + 5kg | 3kg + 5kg + 5kg + 3kg |
| 3kg * 5 vs 5kg * 3 -> min 선택 |
이렇게 하나씩 계산해 나가다 보면 규칙을 발견할 수 있습니다.
바로 인덱스 차이가 3개가 나는 경우 3kg 봉지를 하나 더 들고갈 수 있는 경우가 생기고,
인덱스 차이가 5개가 나는 경우 5kg 봉지를 하나 더 들고갈 수 있습니다.
위의 BOJ 9095 1, 2, 3 더하기와 같은 원리로 찾을 수 있습니다.
즉, 이전에 계산된 값을 저장해두었다가 활용합니다.
처음엔 dp[i-3], dp[i-5] 번째의 수에 + 1 한 수가 dp[i]의 값이 되는 것 같지만, 최소공배수인 15부터는 둘의 대소비교를 해 가며 더 작은 봉지 수를 구해야 합니다.
따라서 경우의 수를 아래와 같이 나눌 수 있습니다.
- dp[i-3], dp[i-5]의 값이 모두 -1일 때
- 가능한 경우의 수가 없는 것 이므로 -1을 저장합니다.
- dp[i-3], dp[i-5] 중 한 개만 -1 일 때(한 개는 -1, 나머지는 가능한 경우의 수 일 때)
- 가능한 경우의 수 + 1 을 저장
- dp[i-3], dp[i-5] 모두 -1이 아닐 때
- 둘 중 더 적은 경우의 수 + 1을 저장
따라서 점화식은 아래와 같이 도출해낼 수 있습니다.
dp[i] = Math.min(dp[i-3], dp[i-5]) + 1;
이를 바탕으로 구현한 소스는 아래와 같습니다.
동적계획법 구현 / 전체 소스 코드
import java.util.Arrays;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner input = new Scanner(System.in);
int n = input.nextInt();
int[] dp = new int[5001];
Arrays.fill(dp, -1);
dp[3] = dp[5] = 1;
for(int i = 6; i <= n; i++) {
if(dp[i-3] == -1 && dp[i-5] == -1) {
continue;
} else if(dp[i-3] == -1 || dp[i-5] == -1) {
dp[i] = Math.max(dp[i-3], dp[i-5]) + 1;
}
else {
dp[i] = Math.min(dp[i-3], dp[i-5]) + 1;
}
}
System.out.println(dp[n]);
}
}이렇게 모든 무게에 대해 DP로 계산해서 결과를 n까지 얻어준 후,
마지막에 구해야하는 결과 값을 print해 줍니다.
이렇게 동적계획법(DP)에 대하여 내용 정리를 해보았습니다.
동적계획법이 다른 알고리즘이랑도 함께 활용하는 방법들이 많아서요,
문제에서 얼마나 DP를 활용해서 내느냐에 따라 난이도가 엄청 차이가 나기도 합니다.
따라서 이번 기회에 기초부터 정리해보았습니다!

오랜만에 알고리즘 문제들을 풀다보니 정리해가며 풀어야겠다는 생각도 들었습니다!ㅎㅎ
저와 같이 알고리즘 문제풀이를 공부하시는 분들께도 도움이 되었으면 좋겠습니다!


